Système de numération et codage binaire
Définitions
- Système de numération : Un système de numération est un ensemble de conventions pour former les nombres, les dire, les écrire et calculer.
Les nombres s'énoncent et peuvent s'écrire (onze, quarante, etc.) mais par soucis de simplifications, lors des manipulations, les nombres sont représentés par une chaîne de caractère ou chaque caractère dispose d'une pondération dépendant de la base de numération (1984 par exemple)
- Base de numération : Une base de numération est un nombre dont on utilise les puissances successives pour former d'autres nombres plus importants.
Dans nos civilisations occidentales la base de numération est la base 10, mais on utilise aussi la base 12 (une douzaine d'oeufs, la base 60 (une heure = 60 minutes). Les romains, les japonais et certaines cultures africaines utilisent ou utilisaient également la base 5...
Polynôme de numération
 Dans un système de numération pondéré de base B, un entier N est représenté par un polynôme qui est de la forme :
Dans un système de numération pondéré de base B, un entier N est représenté par un polynôme qui est de la forme :
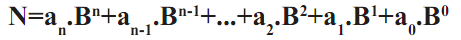
Avec les coefficients an : 0≤ an ≤ B-1
 Par exemple :
Par exemple :
En base 10 1982 est égal à 1000 + 900 + 80 +2 soit
1982 = 1x 103 + 9 x 102 + 8 x 101 + 2 x 100
Cette relation s'applique quel que soit la base B
La base 2
La naissance de l'automatisation a permis de disposer d'équipements disposant de deux états distincts :
- un interrupteur est Ouvert ou Fermé
- un transistor est Passant ou Bloqué lorsqu'il est utilisé en commutation
Ce fonctionnement binaire a contribué à l'utilisation de la base 2 et à la naissance de l'algèbre de Boole.
En codage binaire, chaque poids binaire est représenté par la valeur 0 ou 1.
 Ce poids binaire est appelé Binary Digit en anglais et qui a été contracté en Bit.
Ce poids binaire est appelé Binary Digit en anglais et qui a été contracté en Bit.
En appliquant l'équation polynomiale :
N= an.2n+...+a3.23+a2.22+a1.21+a0.20
Par exemple : 1011 correspond à :
1.23+0.22+1.21+1.20 soit 1.8+0.4+1.2+1.1 = 11
Donc 1011 en base 2 est égal à 11 en base 10
 Le tableau ci-dessous présente l’équivalence décimal/binaire pour les 16 premières valeurs.
Le tableau ci-dessous présente l’équivalence décimal/binaire pour les 16 premières valeurs.
Nombre décimal |
Codage binaire |
|||
8 |
4 |
2 |
1 |
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
2 |
0 |
0 |
1 |
0 |
3 |
0 |
0 |
1 |
1 |
4 |
0 |
1 |
0 |
0 |
5 |
0 |
1 |
0 |
1 |
6 |
0 |
1 |
1 |
0 |
7 |
0 |
1 |
1 |
1 |
8 |
1 |
0 |
0 |
0 |
9 |
1 |
0 |
0 |
1 |
10 |
1 |
0 |
1 |
0 |
11 |
1 |
0 |
1 |
1 |
12 |
1 |
1 |
0 |
0 |
13 |
1 |
1 |
0 |
1 |
14 |
1 |
1 |
1 |
0 |
15 |
1 |
1 |
1 |
1 |
 Un nombre binaire est souvent précédé du caractère % pour préciser la base et le distinguer d'un nombre décimal : %10010101 par exemple.
Un nombre binaire est souvent précédé du caractère % pour préciser la base et le distinguer d'un nombre décimal : %10010101 par exemple.